
It is notĬontinuous in the entire domain because there are discontinuities in the graph. Hence, each sub-function of a step function isĬontinuous, implying that the step function is piecewise continuous. But as long as it meets all of the other requirements (for example, as long as the graph is continuous between the undefined points), it’s still considered piecewise continuous. Therefore, pieces should not intersect or overlap such that it violates the vertical line test. Piecewise function synonyms, Piecewise function pronunciation, Piecewise function translation, English dictionary definition of. Perhaps surprisingly, nothing in the definition states that every point has to be defined.A function could be missing, say, a point at x 0. The absolute value function is a very good example of a piecewise function. The graph of a piecewise function has different pieces corresponding to each of its definitions. The union of each of these domains yields the domain of the main function.į ( x ) = s u b − f u n c t i o n 1, w h e n x i s i n d o m a i n 1 f\left( x \right) = \right] =- 14 = 5, = 2, = − 8, = − 1 4Ĭonstant functions are continuous. Lesson 1: Piecewise Functions def: piecewise function a function composed of 2 or more functions defined by domain restrictions (pieces of functions on the same graph) 10 10 When graphing, we still need to be mindful that our graph is a function. A piecewise function is a function f(x) which has different definitions in different intervals of x. Each equation is valid for some interval. Piecewise Continuous Function A piecewise continuous function is continuous except for a certain number of points. A piecewise-defined function is one which is defined not by a single equation, but by two or more. It may or may not be a continuous function. In this other multiple functions are used to apply on specific intervals. For example, let’s say we want to find f (5) in the following function: Since 5 is greater than 0, the function with which we will use to evaluate f (5) is f(x. Evaluate the value using the corresponding function. More specifically, it’s a function defined over two or more intervals rather than with one simple equation over the domain. A piecewise function is a function, which is defined by various multiple functions. To solve piecewise functions, we have to take into account the following: Check carefully where the x lies in the given interval. Each formula is defined within a particular domain or sub-interval. A piecewise function is a function made up of different parts.
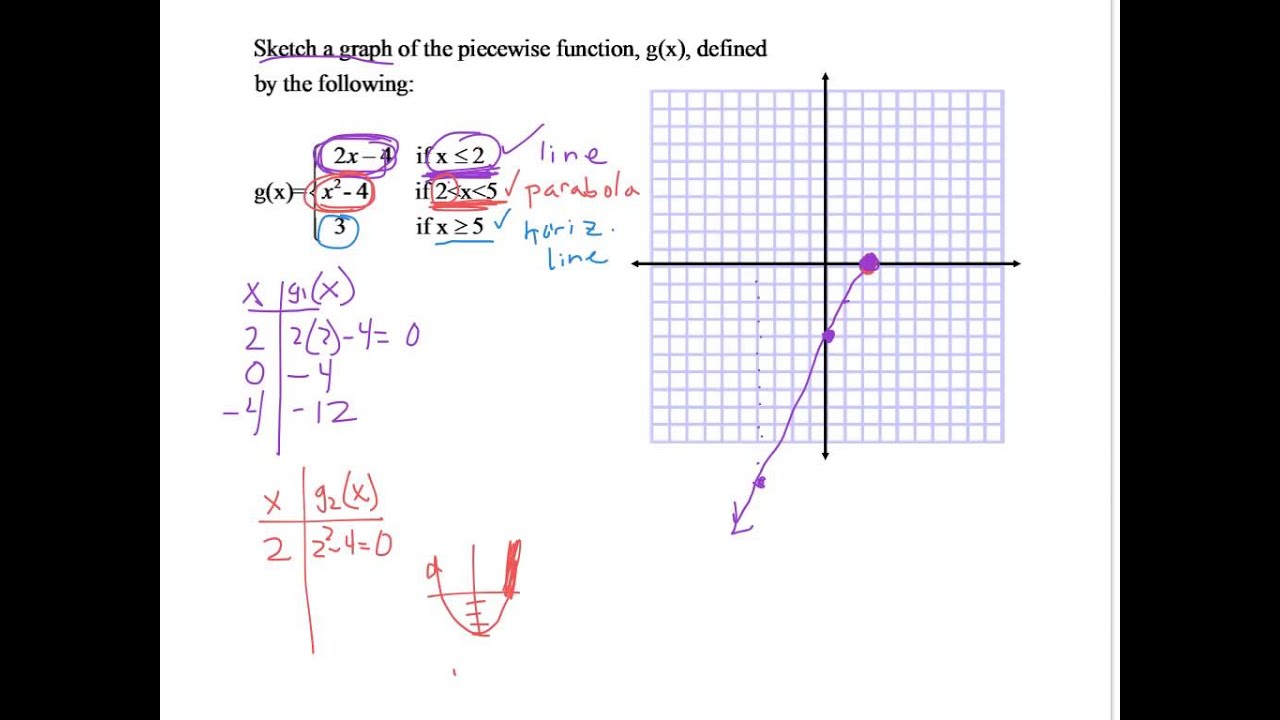

In other words, a piecewise function is one which uses more than one formula or sub-function to define the output.

The Floor Function is a very special piecewise function. It has two pieces: below zero: -x from 0 onwards: x f(x) x The Floor Function. The piecewise definition is a way of expressing the function in different sub-intervals. The Absolute Value Function is a famous Piecewise Function. A piecewise-defined function (also called a piecewise function or a hybrid function) is defined using multiple sub-function (or formula), where each sub-function is defined within a specific sub-interval which is a part of the domain of the main function.


 0 kommentar(er)
0 kommentar(er)
